向量对称是没有关系的,所以可以将两个 $x$ 坐标或两个 $y$ 坐标调整成非负数,以下默认如此。
以 $(0,0)$ 作为一角的两向量合成的平行四边形作为底块覆盖整个平面。
容易发现平行四边形内部和邻边上的点(不包含四个顶点)是无法互相到达的,外加顶点,就能拓展到整个平面。
根据皮克定理 $S=n+\frac{s}{2}-1$,容易发现这些点是数量就是平行四边形的面积,这样是否存在解就可以直接判断了。但如果用计算几何去找出这些点会被卡精度。
不妨钦定起点为 $(0,0)$ 然后往平行原坐标轴的方向走,遇到相同的边就记录一下对应到原坐标系、与走的方向垂直的相对位置。
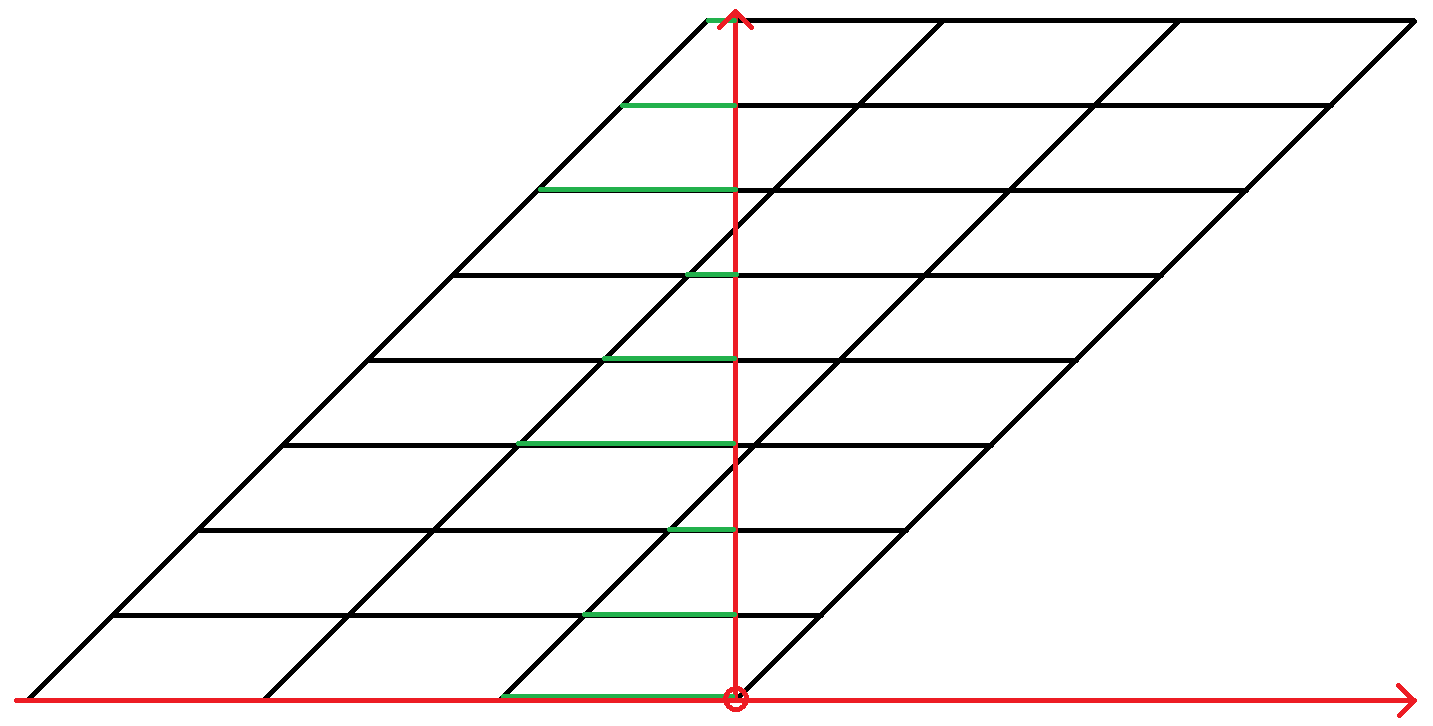
观察它们与一侧顶点的距离,显然可以表示成 $ax_1+bx_2$ 或是 $ay_1+by_2$,并且是一步一步变化的。如果将每种距离都取到恰好一次,就恰好拼成了一个平行四边形,也就找出了解。
根据裴蜀定理,只要将初始的一个点增加至 $\gcd(x_1,x_2)$ 或 $\gcd(y_1,y_2)$ 个点即可。
也就是说任意一个边长为 $\gcd(x_1,x_2)$ 或 $\gcd(y_1,y_2)$ 的面积为 $n$ 的点矩形(不能旋转九十度)都可为解。